Calculus__Differentiation

It's one of those topics whose name when uttered strikes fear in students, ( one of those topics which we have heard about vaguely from our seniors but are scared yet interested to research about.

( One of those topics which might make you wish why the entire branch didn't fall on Newton's head instead of a tiny harmless apple (ง •_•)ง)

Well, In this blog let's dive together and understand this concept ( and maybe also save Newton from the curses of highschoolers 🤣)

Wait! Before we actually start with the calculation part of calculus, Let's answer a very common question asked by us highschoolers when we are stuck in between a solution, ready to pull our hair out

"WHY DO WE HAVE TO LEARN THIS! WHY WHY! " (*hoping the fire your brain in burning in, destroys your physics book*)

Yes, been there, gone through that. So lets me make your learning experience less melodramatic (/▽＼)

1) Calculus is majorly used to calculate the slope of a curve in a graph. And believe it or not, curves in graphs are used alot in many fields including architecture and engineering.

2) Statisticians -- If you know any buisness which is famous and sucessful ( Why, even google for that matter) , that buisness is in debt to Calculus.

3) Movies and Video games -- Yes, you heard me right, Netflix and Minecraft is possible only because of Calculus.

4) Weather predictions and even music! ( Wondering how music can be depended on Calculus? Well, am saving the best for the last so Read on!)

Let's actually start now,

Remember what I said about calculus and graph?

Take the X-Y coordinate system and draw a line in it

The slope of this graph is change in Y axis upon change in X axis, also represented as :-

or as --

Where delta ( the triangle symbol) shows 'change in'

( on closer inspection you will discover is the tan value of the triangle formed by extending the lines) This tan value remains constant at any point of the slope for a straight line.

So, for any graph we should just figure out the initial and final positions of Y and their respective X coordinates and apply the formula to get the slope

This works for a straight line, what do we do when we get a graph like this?

In this case we can't exactly calculate the slope of the entire graph, directly. Consider a point in the curve, and draw a tangent touching the point and the X axis

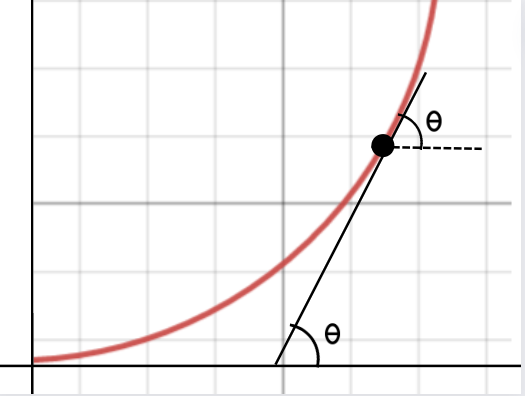
Let the angle formed by the tangent and the X axis be theta.

Hence the slope in that point would be dy/dx (d represents 'very changes' in x and y respectively) Basically, try and draw a teeny-tiny triangle at the point we have considered, the tan value of that small triangle will give slope of the graph at that point.

And this dy/dx can be found out by the wonderful concept of differentiation

For example, let's take the equation of a curve as y = 2x^3 ( two x cube)

To find the slope of this particular graph you have to differentiate the above

How do we solve this problem? , you may ask...

This like any math equation which contains more alphabets than numbers follows few formulas

These are the two most basic formulas used in the process of differentiation, remembering this you can solve alot of questions thrown at you by your maths teacher.

Let's try and solve our example now,

(*tada!*)

SUM OR SUBTRACTION

Ofcouse, in our real life, we won't come across questions which deal with single terms, (to make our lives better or worse) we usually come across questions which deal with the addition or subtraction. But don't worry, we have a simple method to solve them too

Where f(x) and g (x) represent two different equations (functions) in x. ( This is a very fancy way of telling, differentiate them seperately and then add them)

For Example :-

PRODUCT RULE

Remember, when we struggled to find what 13 into 14 was back in 5th grade? Now see us, years later, figuring out products of alphabets and greek letters (。・・)ノ

We should differentiate the first one seperately, multiply it with the second one ( which is undifferentiated) then add this with the product of the first (undifferentiated) on with the second differentiated one. (This might sound crazy at the moment but an example will make it simpler to understand)

Example:-

DIVISION RULE OR QUOTIENT RULE

We did addition, subtraction and multiplication... leaving division out is just bad ( like Roald Dahl said " Never do anything by halves if you want to get away with it. Be outrageous. Go the whole hog" )

Its similar to the multiplication rule but we should make sure to follow the order in this rule.

Example :-

Ig that's enough rules and formulas for one blog right?

Now, back to the point I promised in the start of the blog

How is MUSIC related to calculus?

Music , the thing which lightens our mood when we are sad , pours out emotions and understanding through its rhythm , is just a series of oscillations. A music piece usually follows a particular sequence or series which can be represented in the form of waves. And this wave can be plotted in a graph ( see where I am getting to?)

Major music companies use calculus to record music and use loudspeakers.

So, that's all folks

I feel the perfect way to end a calculus blog is with a calculus joke ( Calculus can make you cry, it can make you laugh, it make you do both at the same time (^///^)

(A relatable one indeed) ☆⌒(*＾-゜)v