How to solve the Schrodinger's Equation
- manthramohana1
- Oct 22, 2022
- 2 min read
The genius austrian scientist ( with a very confusing name to pronounce) shook the world of chemistry by his theories of quantum mechanics. He introduced the concept of 'probability' for finding an atom which changed the entire outlook of how scientists perceived an atom...
From Heisenbergs theory, we know that it's impossible to find the velocity and position of an electron simultaneouly ( don't know this? Click here ! and chk out page 22 ) Hence , the Bohr's model of an atom, which gave defined paths (or orbits) for an atom got ruled out. That is when, the concept of probability of finding a particular electron in a certain region came up which was said to be given by the square of wave function |Ψ|^2 ( that poseidon's trident symbol under modulus is called psi , it is the mathematical description of quantum state of particle including all the quantum numbers . Imagine it to be the detailed address of an electron represented using one complex symbol )
Our guy Schrodinger( bored after torturing his poor cat in a radioactive box, RIP kitty) decided to find an equation relating to this wave function. His trials led to this
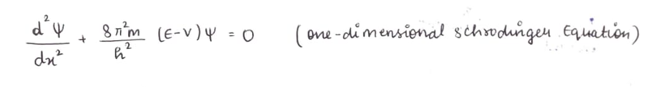
(A big equation with weird symbols right?)
here,
psi- wave funtion
x - represents the coordinate axis ( only along one dimension)
h - planck's constant
E - describes total energy
V - describes potential energy
Schrodinger stated that by solving this ridiculous expression, we can get the value of psi, which in turns gives the delivery address for an electron
Now, how do we solve it? Here's the simplest method

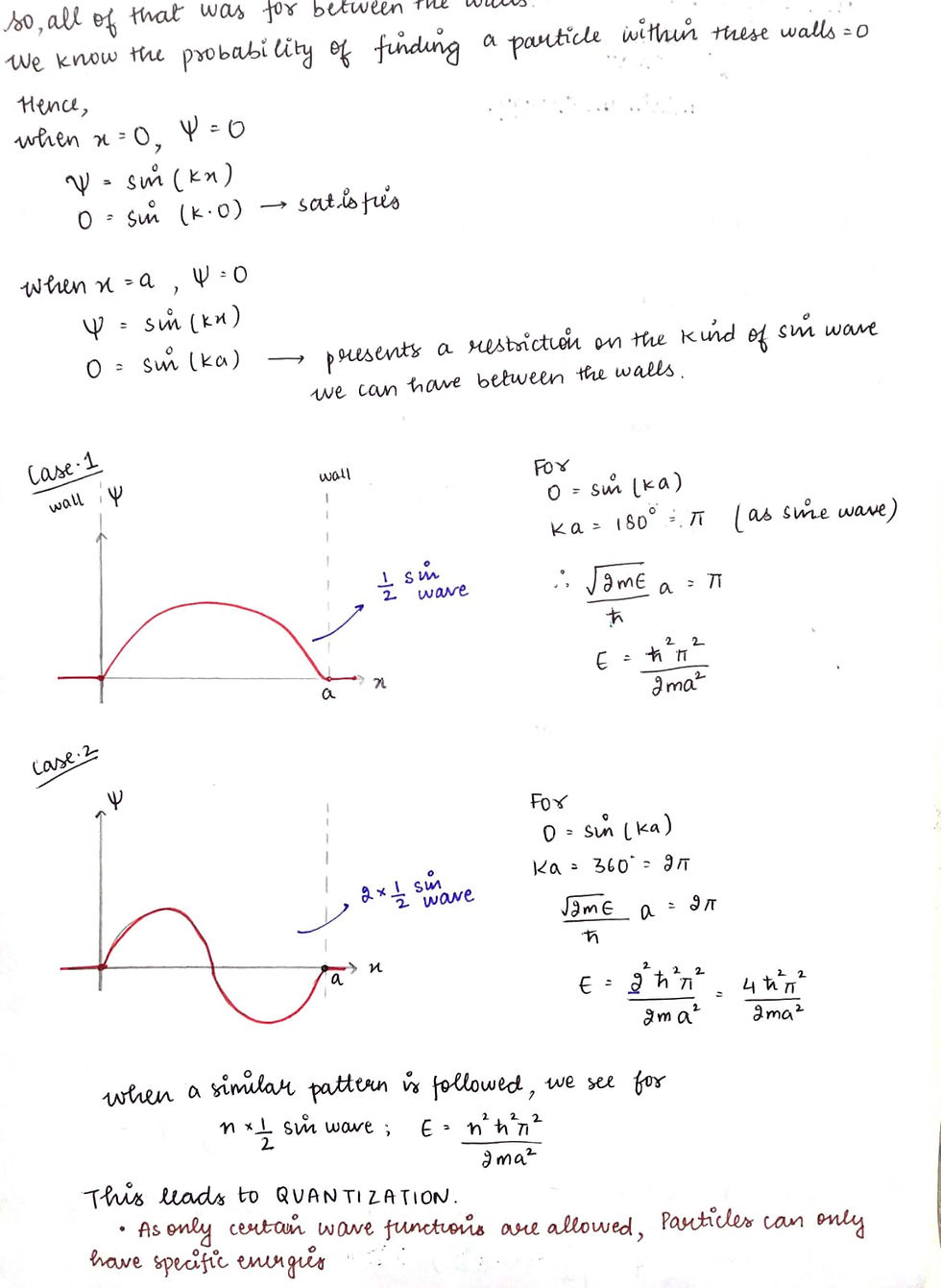

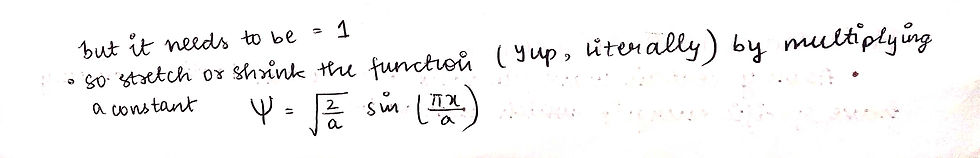
This last bit, where we mulitply the entire equation with under root 2/a is called NORMALISATION
This value further helps us get the 3 quantum numbers :- Prinicpal quantum number. Azimuthal quantum number and the magnetic quantum number!
Congratulations y'all! You just achieved something which was deemed almost impossible!
Now, to celeberate this extraordinary moment , one of my favourite scenes from one of my favourite series which pays a hilarious tribute to our dear friend Planck






Comments